How To Find Slope Rise Over Run
Learning Objectives
- Find the Gradient from a Graph
- Place rise and run from a graph
- Distinguish between graphs of lines with negative and positive slopes
- Find the Slope from Two Points
- Apply the formula for slope to define the slope of a line through ii points
- Find the Slope of Horizontal and Vertical Lines
- Find the slope of the lines [latex]x=a[/latex] and [latex]y=b[/latex]
- Recognize that horizontal lines have gradient = 0
- Recognize that vertical lines take slopes that are undefined
- Identify slopes of parallel and perpendicular lines
- Given a line, identify the slope of another line that is parallel to it
- Given a line, identify the gradient of another line that is perpendicular to it
- Interpret slope in equations and graphs
- Verify the slope of a linear equation given a dataset
- Interpret the slope of a linear equation as information technology applies to a real situation
Identify slope from a graph
The mathematical definition of slope is very similar to our everyday 1. In math, slope is used to describe the steepness and direction of lines. By merely looking at the graph of a line, yous can learn some things nearly its slope, peculiarly relative to other lines graphed on the same coordinate airplane. Consider the graphs of the three lines shown below:
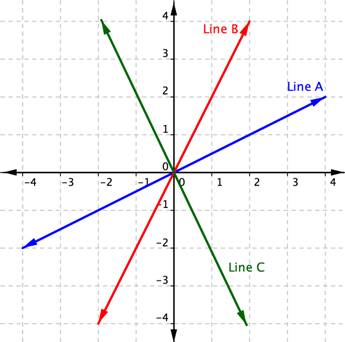
First, permit's look at lines A and B. If you imagined these lines to be hills, you would say that line B is steeper than line A. Line B has a greater gradient than line A.
Next, find that lines A and B slant up as you move from left to correct. Nosotros say these 2 lines have a positive slope. Line C slants downwardly from left to correct. Line C has a negative slope. Using two of the points on the line, you can find the slope of the line past finding the rise and the run. The vertical change between two points is called the ascension, and the horizontal change is called the run. The slope equals the ascension divided past the run: [latex] \displaystyle \text{Slope }=\frac{\text{rise}}{\text{run}}[/latex].
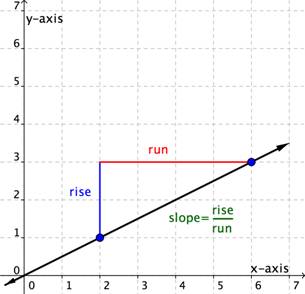
You tin determine the slope of a line from its graph by looking at the rise and run. One characteristic of a line is that its slope is constant all the mode along it. And then, you can cull any two points along the graph of the line to figure out the gradient. Let's look at an case.
Example
Use the graph to detect the slope of the line.
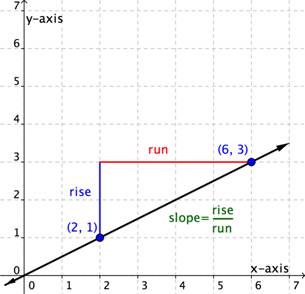
This line will have a slope of [latex] \displaystyle \frac{ane}{2}[/latex] no matter which ii points you pick on the line. Try measuring the gradient from the origin, [latex](0,0)[/latex], to the bespeak [latex](half-dozen,3)[/latex]. You lot volition find that the [latex]\text{rise}=3[/latex] and the [latex]\text{run}=6[/latex]. The gradient is [latex] \displaystyle \frac{\text{rise}}{\text{run}}=\frac{iii}{6}=\frac{ane}{2}[/latex]. It is the aforementioned!
Let'southward look at another example.
Case
Use the graph to find the slope of the two lines.
When you look at the 2 lines, you can run across that the blue line is steeper than the red line. It makes sense the value of the slope of the blue line, iv, is greater than the value of the gradient of the red line, [latex] \displaystyle \frac{1}{iv}[/latex]. The greater the slope, the steeper the line.
Finding the Slope of a Line From a Graph
Distinguish between graphs of lines with negative and positive slopes
Direction is important when it comes to determining gradient. It's of import to pay attention to whether you are moving up, downward, left, or correct; that is, if yous are moving in a positive or negative direction. If you go up to get to your second point, the ascent is positive. If yous go down to go to your second point, the rising is negative. If you go right to become to your 2d bespeak, the run is positive. If you go left to get to your second point, the run is negative.
In the post-obit two examples, you lot will see a gradient that is positive and one that is negative.
Instance (Advanced)
Notice the slope of the line graphed below.
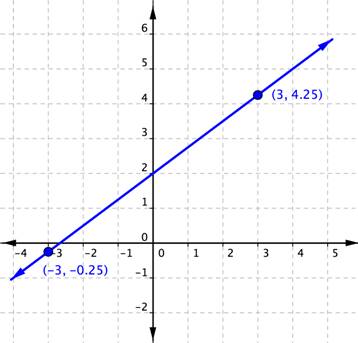
The side by side example shows a line with a negative slope.
Example
Find the gradient of the line graphed beneath.
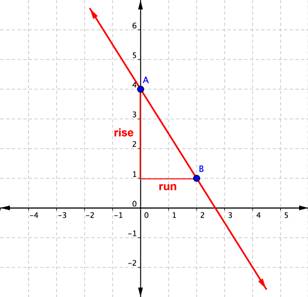
In the example above, y'all could have establish the gradient by starting at point B, running [latex]{-2}[/latex], and so rising [latex]+iii[/latex] to arrive at betoken A. The result is however a slope of [latex]\displaystyle\frac{\text{rise}}{\text{run}}=\frac{+3}{-2}=-\frac{three}{two}[/latex].
Finding the Slope from Two Points on the Line
You've seen that you lot tin can notice the slope of a line on a graph by measuring the rise and the run. You can also find the slope of a straight line without its graph if y'all know the coordinates of any ii points on that line. Every indicate has a set of coordinates: an x-value and a y-value, written as an ordered pair (10, y). The x value tells you where a bespeak is horizontally. The y value tells you lot where the point is vertically.
Consider two points on a line—Signal 1 and Bespeak ii. Point 1 has coordinates [latex]\left(x_{one},y_{i}\right)[/latex] and Point 2 has coordinates [latex]\left(x_{2},y_{two}\correct)[/latex].

The rise is the vertical distance between the 2 points, which is the difference between their y-coordinates. That makes the rise [latex]\left(y_{ii}-y_{1}\right)[/latex]. The run between these two points is the departure in the x-coordinates, or [latex]\left(x_{2}-x_{one}\right)[/latex].
So, [latex] \displaystyle \text{Slope}=\frac{\text{rising}}{\text{run}}[/latex] or [latex] \displaystyle g=\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{i}}}[/latex]
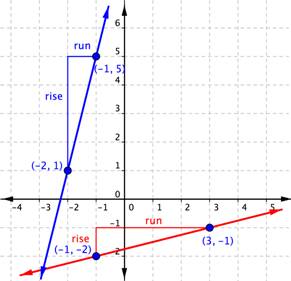
In the example below, yous'll see that the line has 2 points each indicated as an ordered pair. The point [latex](0,2)[/latex] is indicated as Signal ane, and [latex](−2,vi)[/latex] equally Betoken 2. And then you are going to motion from Point 1 to Point 2. A triangle is drawn in above the line to aid illustrate the ascension and run.

Yous tin can run into from the graph that the ascension going from Point i to Point two is 4, considering you lot are moving 4 units in a positive direction (up). The run is [latex]−two[/latex], considering you are and so moving in a negative management (left) 2 units. Using the slope formula,
[latex] \displaystyle \text{Gradient}=\frac{\text{ascension}}{\text{run}}=\frac{four}{-2}=-2[/latex].
You exercise not demand the graph to find the slope. You tin merely use the coordinates, keeping careful track of which is Point i and which is Point 2. Let's organize the information about the two points:
| Name | Ordered Pair | Coordinates |
|---|---|---|
| Point 1 | [latex](0,ii)[/latex] | [latex]\brainstorm{array}{l}x_{ane}=0\\y_{ane}=ii\end{assortment}[/latex] |
| Bespeak 2 | [latex](−ii,6)[/latex] | [latex]\begin{array}{l}x_{2}=-two\\y_{2}=6\terminate{array}[/latex] |
The slope, [latex]m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{vi-two}{-2-0}=\frac{4}{-two}=-2[/latex]. The slope of the line, m, is [latex]−2[/latex].
Information technology doesn't affair which point is designated every bit Point 1 and which is Point 2. You lot could have called [latex](−2,half-dozen)[/latex] Point one, and [latex](0,2)[/latex] Betoken 2. In that case, putting the coordinates into the gradient formula produces the equation [latex]k=\frac{2-vi}{0-\left(-2\right)}=\frac{-4}{2}=-2[/latex]. One time again, the slope is [latex]grand=-ii[/latex]. That's the same slope as before. The important affair is to be consequent when you lot subtract: you must always subtract in the same gild [latex]\left(y_{2},y_{1}\right)[/latex]and [latex]\left(x_{ii},x_{1}\right)[/latex].
Instance
What is the gradient of the line that contains the points [latex](5,5)[/latex] and [latex](4,2)[/latex]?
The example beneath shows the solution when you reverse the gild of the points, calling [latex](5,five)[/latex] Point 1 and [latex](4,ii)[/latex] Point two.
Example
What is the slope of the line that contains the points [latex](five,5)[/latex] and [latex](four,ii)[/latex]?
Detect that regardless of which ordered pair is named Point 1 and which is named Point 2, the slope is notwithstanding 3.
Example (Advanced)
What is the slope of the line that contains the points [latex](3,-six.25)[/latex] and [latex](-1,8.5)[/latex]?
Let'south consider a horizontal line on a graph. No matter which two points you choose on the line, they will always take the same y-coordinate. The equation for this line is [latex]y=three[/latex]. The equation can also be written as [latex]y=\left(0\correct)10+3[/latex].
Video: Finding the Gradient of a Line Given Two Points on the Line
Finding the Slopes of Horizontal and Vertical Lines
So far you've considered lines that run "uphill" or "downhill." Their slopes may be steep or gradual, only they are ever positive or negative numbers. Just there are two other kinds of lines, horizontal and vertical. What is the gradient of a flat line or level ground? Of a wall or a vertical line?

Using the class [latex]y=0x+three[/latex], you lot tin can run across that the gradient is 0. You tin also use the slope formula with two points on this horizontal line to calculate the gradient of this horizontal line. Using [latex](−3,3)[/latex] every bit Point 1 and (2, three) as Point two, you go:
[latex] \displaystyle \begin{array}{fifty}yard=\frac{{{y}_{2}}-{{y}_{1}}}{{{10}_{2}}-{{x}_{one}}}\\\\chiliad=\frac{3-3}{2-\left(-three\right)}=\frac{0}{5}=0\end{assortment}[/latex]
The gradient of this horizontal line is 0.
Allow's consider any horizontal line. No matter which ii points you cull on the line, they will always have the same y-coordinate. So, when you utilize the slope formula, the numerator will always be 0. Zero divided by any not-zilch number is 0, and so the slope of whatsoever horizontal line is always 0.
The equation for the horizontal line [latex]y=3[/latex] is telling y'all that no matter which ii points you cull on this line, the y-coordinate will always be 3.
How about vertical lines? In their case, no affair which two points you choose, they will e'er accept the same x-coordinate. The equation for this line is [latex]x=2[/latex].

There is no way that this equation can be put in the slope-point grade, as the coefficient of y is [latex]0\left(10=0y+2\right)[/latex].
So, what happens when you utilize the slope formula with two points on this vertical line to calculate the gradient? Using [latex](2,one)[/latex] equally Point 1 and [latex](2,three)[/latex] as Point ii, you get:
[latex] \displaystyle \begin{assortment}{50}m=\frac{{{y}_{2}}-{{y}_{1}}}{{{ten}_{two}}-{{x}_{one}}}\\\\m=\frac{iii-1}{2-2}=\frac{2}{0}\end{array}[/latex]
But sectionalization past zero has no meaning for the set of existent numbers. Because of this fact, it is said that the slope of this vertical line is undefined. This is true for all vertical lines—they all have a slope that is undefined.
Example
What is the slope of the line that contains the points [latex](3,2)[/latex] and [latex](−8,2)[/latex]?
Finding Slopes of Horizontal and Vertical Lines
Narrate the slopes of parallel and perpendicular lines
When you graph two or more than linear equations in a coordinate aeroplane, they generally cantankerous at a point. However, when 2 lines in a coordinate airplane never cross, they are chosen parallel lines. You will also look at the case where ii lines in a coordinate plane cross at a right angle. These are called perpendicular lines. The slopes of the graphs in each of these cases have a special relationship to each other.
Parallel lines are two or more lines in a plane that never intersect. Examples of parallel lines are all around us, such as the reverse sides of a rectangular movie frame and the shelves of a bookcase.

Perpendicular lines are 2 or more lines that intersect at a xc-degree bending, like the two lines fatigued on this graph. These xc-degree angles are also known equally right angles.

Perpendicular lines are besides everywhere, not just on graph paper merely also in the world around the states, from the crossing pattern of roads at an intersection to the colored lines of a plaid shirt.
Parallel Lines
Two non-vertical lines in a plane are parallel if they have both:
- the aforementioned slope
- different y-intercepts
Whatever two vertical lines in a airplane are parallel.
Example
Discover the slope of a line parallel to the line [latex]y=−3x+4[/latex].
Example
Make up one's mind whether the lines [latex]y=6x+v[/latex] and [latex]y=6x–i[/latex] are parallel.
Perpendicular Lines
Two not-vertical lines are perpendicular if the gradient of one is the negative reciprocal of the slope of the other. If the slope of the showtime equation is four, and so the gradient of the 2nd equation will need to be [latex]-\frac{1}{iv}[/latex] for the lines to be perpendicular.
You can also cheque the two slopes to meet if the lines are perpendicular by multiplying the two slopes together. If they are perpendicular, the product of the slopes will be [latex]−1[/latex]. For example, [latex] 4\cdot-\frac{1}{4}=\frac{four}{1}\cdot-\frac{1}{iv}=-1[/latex].
Case
Observe the slope of a line perpendicular to the line [latex]y=2x–6[/latex].
To detect the slope of a perpendicular line, discover the reciprocal, [latex] \displaystyle \tfrac{i}{2}[/latex], and and so find the opposite of this reciprocal [latex] \displaystyle -\tfrac{1}{2}[/latex].
Annotation that the product [latex]2\left(-\frac{one}{2}\correct)=\frac{2}{1}\left(-\frac{1}{2}\right)=-1[/latex], so this means the slopes are perpendicular.
In the example where one of the lines is vertical, the gradient of that line is undefined and it is non possible to calculate the product with an undefined number. When one line is vertical, the line perpendicular to it volition exist horizontal, having a slope of zero ([latex]m=0[/latex]).
Instance
Determine whether the lines [latex]y=−8x+v[/latex] and [latex] \displaystyle y\,\text{=}\,\,\frac{1}{eight}ten-1[/latex] are parallel, perpendicular, or neither.
The Gradient of Parallel and Perpendicular Lines
Verify Slope From a Dataset
Massive amounts of data is existence collected every day by a wide range of institutions and groups. This data is used for many purposes including business organisation decisions about location and marketing, authorities decisions nigh allocation of resources and infrastructure, and personal decisions near where to live or where to buy food.
In the following case, you will meet how a dataset can be used to define the slope of a linear equation.
Example
Given the dataset, verify the values of the slopes of each equation.
Linear equations describing the modify in median habitation values between 1950 and 2000 in Mississippi and Hawaii are as follows:
Hawaii: [latex]y=3966x+74,400[/latex]
Mississippi:[latex]y=924x+25,200[/latex]
The equations are based on the following dataset.
x = the number of years since 1950, and y = the median value of a house in the given state.
| Year (x) | Mississippi Firm Value (y) | Hawaii Firm Value (y) |
|---|---|---|
| 0 | $25,200 | $74,400 |
| 50 | $71,400 | $272,700 |
The slopes of each equation can be calculated with the formula you learned in the department on gradient.
[latex] \displaystyle m=\frac{{{y}_{ii}}-{{y}_{one}}}{{{x}_{2}}-{{x}_{1}}}[/latex]
Mississippi:
| Proper name | Ordered Pair | Coordinates |
|---|---|---|
| Point 1 | (0, 25,200) | [latex]\begin{array}{fifty}x_{ane}=0\\y_{i}=25,200\cease{array}[/latex] |
| Point 2 | (50, 71,400) | [latex]\begin{array}{l}x_{two}=fifty\\y_{2}=71,400\end{array}[/latex] |
[latex] \displaystyle one thousand=\frac{{71,400}-{25,200}}{{fifty}-{0}}=\frac{{46,200}}{{50}} = 924[/latex]
We have verified that the gradient [latex] \displaystyle m = 924[/latex] matches the dataset provided.
Hawaii:
| Name | Ordered Pair | Coordinates |
|---|---|---|
| Point 1 | (0, 74,400) | [latex]\begin{assortment}{l}x_{1}=1950\\y_{i}=74,400\cease{array}[/latex] |
| Bespeak two | (fifty, 272,700) | [latex]\begin{array}{fifty}x_{2}=2000\\y_{two}=272,700\stop{array}[/latex] |
[latex]\displaystyle 1000=\frac{{272,700}-{74,400}}{{fifty}-{0}}=\frac{{198,300}}{{fifty}} = 3966[/latex]
We have verified that the slope [latex] \displaystyle m = 3966[/latex] matches the dataset provided.
Example
Given the dataset, verify the values of the slopes of the equation.
A linear equation describing the change in the number of high schoolhouse students who smoke, in a group of 100, between 2011 and 2015 is given as:
[latex]y = -1.75x+xvi[/latex]
And is based on the data from this table, provided by the Centers for Disease Control.
x = the number of years since 2011, and y = the number of high schoolhouse smokers per 100 students.
| Year | Number of Loftier School Students Smoking Cigarettes (per 100) |
| 0 | sixteen |
| 4 | nine |
| Name | Ordered Pair | Coordinates |
|---|---|---|
| Point 1 | (0, 16) | [latex]\begin{assortment}{50}x_{one}=0\\y_{1}=16\end{array}[/latex] |
| Bespeak 2 | (4, nine) | [latex]\begin{array}{fifty}x_{two}=4\\y_{2}=nine\finish{array}[/latex] |
[latex] \displaystyle yard=\frac{{{y}_{two}}-{{y}_{1}}}{{{10}_{2}}-{{x}_{1}}}=\frac{{ix-sixteen}}{{4-0}} =\frac{{-7}}{{4}}=-1.75[/latex]
Nosotros have verified that the slope [latex] \displaystyle{m=-1.75}[/latex] matches the dataset provided.
Interpret the Slope of Linear Equation
Okay, now we take verified that data can provide us with the slope of a linear equation. So what? We tin can use this information to describe how something changes using words.
Kickoff, let's review the different kinds of slopes possible in a linear equation.

We ofttimes utilise specific words to describe the different types of slopes when we are using lines and equations to represent "existent" situations. The following tabular array pairs the type of slope with the common linguistic communication used to describe it both verbally and visually.
| Type of Slope | Visual Description | Verbal Description |
| positive | uphill | increasing |
| negative | downhill | decreasing |
| 0 | horizontal | constant |
| undefined | vertical | N/A |
Case
Interpret the slope of each equation for firm values using words.
Hawaii: [latex]y = 3966x+74,400[/latex]
Mississippi:[latex]y = 924x+25,200[/latex]
Translate the Meaning of the Slope Given a Linear Equation—Median Home Values
Case
Interpret the slope of the line describing the change in the number of high school smokers using words.
Utilise units to the formula for slope. The x values stand for years, and the y values represent the number of smokers. Call up that this dataset is per 100 high schoolhouse students.
[latex] \displaystyle k=\frac{{9-sixteen}}{{2015-2011}} =\frac{{-7 \text{ smokers}}}{{four\text{ year}}}=-one.75\frac{\text{ smokers}}{\text{ year}}[/latex]
The gradient of this linear equation is negative, so this tells u.s.a. that there is a subtract in the number of high school age smokers each year.
The number of loftier schoolers that smoke decreases past 1.75 per 100 each year.
Interpret the Meaning of the Slope of a Linear Equation—Smokers
On the side by side folio, we will meet how to interpret the y-intercept of a linear equation, and make a prediction based on a linear equation.
Summary
Slope describes the steepness of a line. The slope of any line remains constant along the line. The slope tin likewise tell you information about the direction of the line on the coordinate airplane. Slope can be calculated either by looking at the graph of a line or past using the coordinates of any ii points on a line. There are two common formulas for slope: [latex] \displaystyle \text{Slope }=\frac{\text{rise}}{\text{run}}[/latex] and [latex] \displaystyle m=\frac{{{y}_{2}}-{{y}_{i}}}{{{ten}_{2}}-{{x}_{1}}}[/latex] where [latex]m=\text{gradient}[/latex] and [latex] \displaystyle ({{x}_{one}},{{y}_{one}})[/latex] and [latex] \displaystyle ({{x}_{2}},{{y}_{2}})[/latex] are two points on the line.
The images below summarize the slopes of different types of lines.

Source: https://courses.lumenlearning.com/suny-beginalgebra/chapter/read-or-watch-find-slope-from-a-graph/
Posted by: alleneaunded1981.blogspot.com


0 Response to "How To Find Slope Rise Over Run"
Post a Comment